A Comprehensive Guide to Python Linked Lists and Cycle Detection

Linked lists are a foundational data structure used in computer science. They are made up of nodes where each node stores data and a reference (or pointer) to the next node. While Python’s built-in list type handles many dynamic array tasks, understanding how to implement and manipulate linked lists is crucial for mastering data structures and algorithms.

In this blog, we will explore:

Different types of linked lists (singly, doubly, and circular)
How to compare nodes for equality
Advanced linked list operations and algorithms
A detailed explanation and proof of Floyd’s cycle detection (fast and slow pointers) algorithm

1. Types of Linked Lists in Python

1.1 Singly Linked List

Concept: In a singly linked list, each node contains data and a pointer to the next node. This structure is great for scenarios where dynamic memory allocation is needed and where insertions and deletions are frequent.Python Implementation:

# Node class for singly linked list
class Node:
    def __init__(self, data):
        self.data = data  # The data stored in the node
        self.next = None  # Pointer to the next node

# Singly linked list class with basic operations
class LinkedList:
    def __init__(self):
        self.head = None  # Start with an empty list

    # Append a node at the end
    def append(self, data):
        new_node = Node(data)
        if not self.head:
            self.head = new_node
            return
        current = self.head
        while current.next:
            current = current.next
        current.next = new_node

    # Display the linked list
    def display(self):
        current = self.head
        while current:
            print(current.data, end=" -> ")
            current = current.next
        print("None")

1.2 Doubly Linked List

Concept: A doubly linked list has nodes that contain a pointer to both the next node and the previous node. This bidirectional traversal is particularly useful for certain operations like deletion or reverse traversal.Python Implementation:

# Node class for doubly linked list
class DNode:
    def __init__(self, data):
        self.data = data
        self.prev = None  # Pointer to the previous node
        self.next = None  # Pointer to the next node

# Doubly linked list class with basic operations
class DoublyLinkedList:
    def __init__(self):
        self.head = None

    # Append a node at the end
    def append(self, data):
        new_node = DNode(data)
        if not self.head:
            self.head = new_node
            return
        current = self.head
        while current.next:
            current = current.next
        current.next = new_node
        new_node.prev = current

    # Display list from head to tail
    def display_forward(self):
        current = self.head
        while current:
            print(current.data, end=" <-> ")
            current = current.next
        print("None")

    # Display list from tail to head
    def display_backward(self):
        current = self.head
        if not current:
            print("None")
            return
        while current.next:
            current = current.next
        while current:
            print(current.data, end=" <-> ")
            current = current.prev
        print("None")

1.3 Circular Linked List

Concept: In a circular linked list, the last node points back to the head, forming a closed loop. This structure is useful in scenarios where you need to repeatedly loop through the list, such as in round-robin scheduling or the Josephus problem.Python Implementation:

# Node class (same as for singly linked list)
class Node:
    def __init__(self, data):
        self.data = data
        self.next = None

# Circular linked list class
class CircularLinkedList:
    def __init__(self):
        self.head = None

    # Append a node to the circular linked list
    def append(self, data):
        new_node = Node(data)
        if not self.head:
            self.head = new_node
            new_node.next = self.head  # Create the loop
        else:
            current = self.head
            while current.next != self.head:
                current = current.next
            current.next = new_node
            new_node.next = self.head

    # Display the circular linked list
    def display(self):
        if not self.head:
            print("None")
            return
        current = self.head
        while True:
            print(current.data, end=" -> ")
            current = current.next
            if current == self.head:
                break
        print("(Back to head)")

2. Comparing Two Nodes for Equality

When comparing two nodes, there are two main approaches:

2.1 Identity Comparison

By default, using == in Python compares the identity (memory address) of objects. This means that two different node instances with identical data will not be considered equal.

a = Node(10)
b = Node(10)
print(a == b)  # Outputs: False, because they are different objects in memory.

2.2 Structural (Content) Comparison

To compare the content of two nodes (e.g., their stored data), you can override the __eq__ method. This way, if the data in both nodes is the same, they can be considered equal.

class Node:
    def __init__(self, data):
        self.data = data
        self.next = None

    def __eq__(self, other):
        if not isinstance(other, Node):
            return False
        return self.data == other.data

a = Node(10)
b = Node(10)
print(a == b)  # Outputs: True, because their data is equal.

3. Advanced Linked List Algorithms

Beyond basic operations, linked lists support a variety of advanced algorithms:

3.1 Reversing a Linked List

A common interview problem is to reverse a linked list by changing the direction of the pointers.

def reverse_linked_list(head):
    prev = None
    current = head
    while current:
        next_node = current.next  # Save the next node
        current.next = prev       # Reverse the pointer
        prev = current            # Move prev to the current node
        current = next_node       # Proceed to the next node
    return prev  # New head of the reversed list

3.2 Cycle Detection with Floyd’s Algorithm

Floyd’s cycle detection algorithm uses two pointers—a slow pointer that moves one step at a time and a fast pointer that moves two steps. If there is a cycle, the two pointers will eventually meet.

def has_cycle(head):
    slow = head
    fast = head
    while fast and fast.next:
        slow = slow.next           # Move slow pointer one step
        fast = fast.next.next      # Move fast pointer two steps
        if slow == fast:
            return True            # Cycle detected
    return False

3.3 Merging Two Sorted Linked Lists

Merging two sorted lists can be achieved using two pointers, comparing values and linking nodes in sorted order.

def merge_two_sorted_lists(l1, l2):
    dummy = Node(0)
    tail = dummy
    while l1 and l2:
        if l1.data < l2.data:
            tail.next = l1
            l1 = l1.next
        else:
            tail.next = l2
            l2 = l2.next
        tail = tail.next
    tail.next = l1 if l1 else l2
    return dummy.next

3.4 Finding the Middle Node

Using two pointers where one moves twice as fast as the other, you can efficiently locate the middle of a linked list.

def find_middle_node(head):
    slow = head
    fast = head
    while fast and fast.next:
        slow = slow.next
        fast = fast.next.next
    return slow  # Slow pointer will be at the middle

4. Problems Easy

Leetcode 83. Remove Duplicates from Sorted List

class Solution:
    def deleteDuplicates(self, head: Optional[ListNode]) -> Optional[ListNode]:
        if not head:
            return head
        while head.next:
            if head.val == head.next.val:
                head.next = head.next.next
            else:
                head = head.next
        return head

Leetcode 141: Linked List Cycle

Use slow and quick pointers

class Solution:
    def hasCycle(self, head: Optional[ListNode]) -> bool:
        slow, quick = head, head
        while quick and quick.next:
            slow = slow.next
            quick = quick.next.next
            if slow == quick:
                return True
        return False

Use set

class Solution:
    def hasCycle(self, head: Optional[ListNode]) -> bool:
        seen = set()
        while head:
            if head in seen:
                return True
            seen.add(head)
            head = head.next
        return False

Modify node

class Solution:
    def hasCycle(self, head: Optional[ListNode]) -> bool:
        curr = head
        while curr:
            if curr.val == 'visited':
                return True
            curr.val = 'visited'
            curr = curr.next
        return False

160. Intersection of Two Linked Lists

Given the heads of two singly linked-lists headA and headB, return the node at which the two lists intersect. If the two linked lists have no intersection at all, return null.

For example, the following two linked lists begin to intersect at node c1

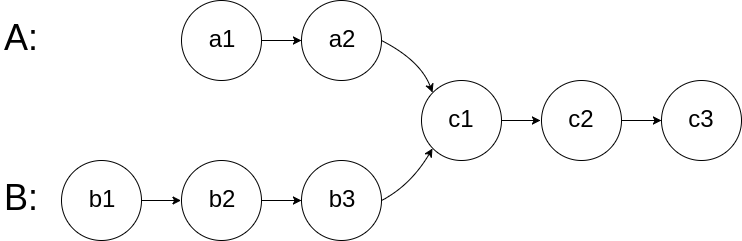
The test cases are generated such that there are no cycles anywhere in the entire linked structure.

Note that the linked lists must retain their original structure after the function returns. Example

output: 8

Solution:

class Solution:
    def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> Optional[ListNode]:
        curr_a, curr_b = headA, headB
        while curr_a != curr_b:
            curr_a = curr_a.next if curr_a else headB
            curr_b = curr_b.next if curr_b else headA
        return curr_a

Explanation: This two-pointer approach works by:

Traversing both lists simultaneously
When reaching the end of a list, continuing from the head of the other list
Meeting at the intersection point after O(m + n) iterations
Handling non-intersecting cases by eventually both pointing to null

Example: For two lists A → B → C → D and X → C → D (intersecting at C):

curr_a path: A → B → C → D → X → C curr_b path: X → C → D → A → B → C Both meet at C after 5 steps.

Complexity:

Time: O(m + n) - Each pointer traverses both lists once.
Space: O(1) - No additional data structures used.

203 Remove Linked List Elements

Problem: https://leetcode.com/problems/remove-linked-list-elements/description/

Example 1:

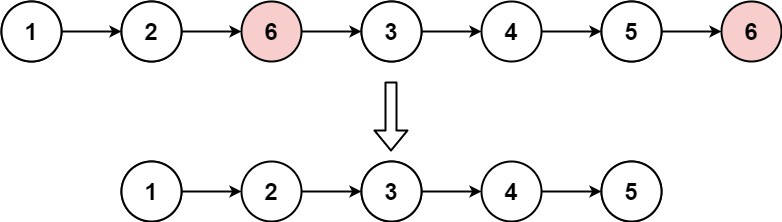
Input: head = [1,2,6,3,4,5,6], val = 6
Output: [1,2,3,4,5]

Example 2:

Input: head = [], val = 1
Output: []

Example 3:

Input: head = [7,7,7,7], val = 7
Output: []

Solution:

class Solution:
    def removeElements(self, head: Optional[ListNode], val: int) -> Optional[ListNode]:
        dummy = ListNode(0, head) # add a dummy head
        prev, curr = dummy, head
        while curr:
            if curr.val == val:
                prev.next = curr.next
            else:
                prev = curr
            curr = curr.next
        return dummy.next

Explanation:

Dummy Head Pattern:
Creates a temporary head node to handle edge cases where the real head needs removal
Eliminates special cases for empty lists or head node removal
Two-Pointer Technique:
prev tracks the last valid node
curr examines current node
When finding target value: prev.next skips over curr
Otherwise: prev advances normally
Iteration Logic:
Always advances curr to next node
Only advances prev when keeping current node

Complexity:

Time: O(n) - Single pass through all nodes
Space: O(1) - Constant extra space for pointers

206 Reverse Linked List

Problem: https://leetcode.com/problems/reverse-linked-list/description/

Example 1:

Input: head = [1,2,3,4,5]
Output: [5,4,3,2,1]

Solution:

class Solution:
    def reverseList(self, head: Optional[ListNode]) -> Optional[ListNode]:
        dumpy_head =ListNode(0,None)
        current = head
        while current:
            next_node = current.next
            current.next = dumpy_head.next
            dumpy_head.next = current
            current = next_node
        return dumpy_head.next

Explanation:

Dummy Head Technique:
Creates a temporary head to build the reversed list
Initial empty reversed list: dummy_head → None
Iterative Reversal Process:
Preserve next_node before modifying links
Insert current node at front of reversed list:
- current.next points to previous reversed head
- Update dummy_head's next to current node
Move to next node in original list
Visualization:
Original: 1 → 2 → 3 → None
After 1st iteration: dummy → 1 → None
After 2nd: dummy → 2 → 1 → None
Final: dummy → 3 → 2 → 1 → None

Complexity:

Time: O(n) - Single pass through all nodes
Space: O(1) - Constant extra space for pointers

234 Palindrome Linked List

Problem: https://leetcode.com/problems/palindrome-linked-list/description/

Given the head of a singly linked list, return true if it is a palindrome or false otherwise.

Example 1:

Input: head = [1,2,2,1]
Output: true

Example 2:

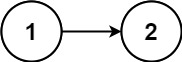
Input: head = [1,2]
Output: false

Solution:

class Solution:
    def isPalindrome(self, head: Optional[ListNode]) -> bool:
        """use idea from reverse linked list"""
        slow, fast = head, head
        while fast and fast.next:
            slow = slow.next
            fast = fast.next.next
        prev, curr = None, slow
        while curr:
            next_node = curr.next
            curr.next = prev
            prev = curr
            curr = next_node
        left, right = head, prev
        while right:
            if left.val != right.val:
                return False
            left = left.next
            right = right.next
        return True

Explanation:

Midpoint Identification:
Fast & slow pointers find middle (slow stops at n/2)
For odd lengths: slow skips center node (not compared)
Reverse Second Half:
Reverse nodes starting from slow pointer
Creates reversed tail: e.g. 1→2→3→2→1 becomes 1→2→3←2←1
Two-Way Comparison:
left starts at head, right starts at reversed tail
Compare node values moving towards center
Mismatch at any point → not palindrome

Complexity:

Time: O(n) - Three sequential passes (find mid + reverse + compare)
Space: O(1) - In-place reversal, no extra storage

705. Design HashSet

Problem

Design a HashSet without using any built-in hash table libraries.

Implement MyHashSet class:

void add(key) Inserts the value key into the HashSet. bool contains(key) Returns whether the value key exists in the HashSet or not. void remove(key) Removes the value key in the HashSet. If key does not exist in the HashSet, do nothing.

Solution:

class ListNode:
    def __init__(self, val=-1, next=None):
        self.val = val
        self.next = next

class MyHashSet:
    def __init__(self):
        self.size = 1009  # Prime number for better hash distribution
        self.buckets = [ListNode() for _ in range(self.size)]

    def _hash(self, key: int) -> int:
        return key % self.size

    def add(self, key: int) -> None:
        h = self._hash(key)
        curr = self.buckets[h]
        while curr.next:
            if curr.next.val == key:
                return  # Key already exists
            curr = curr.next
        curr.next = ListNode(key)

    def remove(self, key: int) -> None:
        h = self._hash(key)
        curr = self.buckets[h]
        while curr.next:
            if curr.next.val == key:
                curr.next = curr.next.next
                return
            curr = curr.next

    def contains(self, key: int) -> bool:
        h = self._hash(key)
        curr = self.buckets[h].next
        while curr:
            if curr.val == key:
                return True
            curr = curr.next
        return False

Explanation:

Hash Function & Buckets:
Uses a prime number (1009) of buckets to reduce collisions
key % size distributes keys across buckets
Add Operation:
Finds bucket using hash function
Checks for existing key in linked list
Appends new node if key doesn't exist
Remove Operation:
Traverses bucket's linked list
Removes node by bypassing its reference
Contains Check:
Searches only within the relevant bucket
Returns True immediately upon finding key

Complexity:

Average Case: O(1) for all operations
Worst Case: O(n) (all keys collide)
Space: O(n + buckets)

706. Design HashMap

● Easy

Design a HashMap without using any built-in hash table libraries.

Implement the MyHashMap class:

MyHashMap() initializes the object with an empty map.
void put(int key, int value) inserts a (key, value) pair into the HashMap. If the key already exists in the map, update the corresponding value.
int get(int key) returns the value to which the specified key is mapped, or -1 if this map contains no mapping for the key.
void remove(key) removes the key and its corresponding value if the map contains the mapping for the key.

class ListNode:
    def __init__(self, key=-1, value=-1, next=None):
        self.key = key
        self.value = value
        self.next = next

class MyHashMap:
    def __init__(self):
        self.size = 1009
        self.buckets = [ListNode() for _ in range(self.size)]

    def _hash(self, key: int) -> int:
        return key % self.size

    def put(self, key: int, value: int) -> None:
        h = self._hash(key)
        curr = self.buckets[h]
        while curr.next:
            if curr.next.key == key:
                curr.next.value = value
                return
            curr = curr.next
        curr.next = ListNode(key, value)

    def get(self, key: int) -> int:
        h = self._hash(key)
        curr = self.buckets[h].next
        while curr:
            if curr.key == key:
                return curr.value
            curr = curr.next
        return -1

    def remove(self, key: int) -> None:
        h = self._hash(key)
        curr = self.buckets[h]
        while curr.next:
            if curr.next.key == key:
                curr.next = curr.next.next
                return
            curr = curr.next

Explanation of the HashMap Implementation:

Core Components:
Buckets: 1009 linked lists (prime number reduces collisions)
Hash Function: Simple modulo operation (key % size)
ListNode: Stores key-value pairs and next pointer
Key Operations:
Put: Finds bucket via hash Updates value if key exists Appends new node if key is new
Get: Searches bucket's linked list Returns -1 if not found
Remove: Uses dummy head for safe deletion Bypasses target node's reference Complexity Analysis:
Time:
Average: O(1) with good hash distribution
Worst: O(n) (all keys collide)
Space: O(n + buckets)

Comparison with Built-in Hash Tables:

Feature	This Implementation	Python dict
Collision Handling	Linked List Chaining	Open Addressing
Load Factor Control	Fixed Size	Dynamic Resizing
Hash Function	Simple Modulo	Complex (CPython)
Memory Overhead	Higher (Nodes + Links)	Lower (Dense Array)
Worst-Case Lookup	O(n)	O(1)
Built-in Methods	Limited (put/get/remove)	Extensive
Performance (Average)	~3x slower	Optimized C Code

876. Middle of the Linked List

Problem: https://leetcode.com/problems/middle-of-the-linked-list/

Given the head of a singly linked list, return the middle node. If there are two middle nodes, return the second one.

Solution Code:

class Solution:
    def middleNode(self, head: Optional[ListNode]) -> Optional[ListNode]:
        slow = fast = head
        while fast and fast.next:
            slow = slow.next
            fast = fast.next.next
        return slow

alt text

Explanation:

Two-Pointer Technique (Tortoise & Hare):
Initialize slow and fast pointers at head
Move slow by 1 node, fast by 2 nodes per iteration
When fast reaches end, slow points to middle
Edge Cases:
Single node: Returns head directly
Even nodes: Returns second middle (e.g., 4 in 1→2→3→4→5→6)
Complexity Analysis:
Time: O(n) - Single traversal
Space: O(1) - Constant pointer variables

Example Walkthrough:

Input: 1 → 2 → 3 → 4 → 5
Step 1: slow=1, fast=1
Step 2: slow=2, fast=3
Step 3: slow=3, fast=5
(fast.next=None → stop)
Output: Node with value 3
Input: 1 → 2 → 3 → 4 → 5 → 6
Step 1: slow=1, fast=1
Step 2: slow=2, fast=3
Step 3: slow=3, fast=5
Step 4: slow=4, fast=None (exit loop)
Output: Node with value 4

1290 Convert Binary Number in a Linked List to Integer

https://leetcode.com/problems/convert-binary-number-in-a-linked-list-to-integer/description/

Given head which is a reference node to a singly-linked list. The value of each node in the linked list is either 0 or 1. The linked list holds the binary representation of a number.

Return the decimal value of the number in the linked list.

The most significant bit is at the head of the linked list.

Example

Input: head = [1,0,1]
Output: 5
Explanation: (101) in base 2 = (5) in base 10

Solution

def getDecimalValue(self, head: Optional[ListNode]) -> int:
    current = head
    rst = 0
    while current:
        rst = 2*rst+current.val
        current = current.next
    return rst

alt text

Explanation:

Initialization:
current pointer starts at the head of the list
rst (result) is initialized to 0
Traversal and Conversion:
Traverse each node in the linked list
For each node, update rst using the formula: rst = 2 * rst + current.val
- This effectively shifts rst left by one bit (multiplying by 2) and adds the current node's value
Move current to the next node
Final Result:
Once traversal is complete, rst contains the decimal value of the binary number

Example:

For input list 1 → 0 → 1:
Step 1: rst = 0, current.val = 1 → rst = 2*0 + 1 = 1
Step 2: rst = 1, current.val = 0 → rst = 2*1 + 0 = 2
Step 3: rst = 2, current.val = 1 → rst = 2*2 + 1 = 5
Output: 5 (binary 101 to decimal)

Complexity:

Time: O(n) - Single pass through the list
Space: O(1) - Constant space usage