LeetCode 18: 4Sum
Problem Overview 🤔
The 4Sum problem is a classic array manipulation challenge that builds upon the concepts of Two Sum and Three Sum. Let's break down what we're trying to solve!
Given an array nums of n integers and a target value, we need to find all unique quadruplets that sum up to the target. It's like finding four puzzle pieces that fit perfectly together! 🧩
Problem Constraints
The Journey to an Optimal Solution 🚀
Let's explore different approaches to solve this problem, starting from a basic solution and gradually optimizing it. Each solution brings something unique to the table!
Solution 1: Recursive Approach with Early Pruning 🌳
Our first solution takes a recursive approach, breaking down the 4Sum problem into smaller subproblems. Think of it like a tree where each level represents one number in our quadruplet.
Key Insights:
- 🔍 Sort the array first to handle duplicates and enable pruning
- 🚫 Early pruning using sum checks
- 🔄 Recursive reduction from 4Sum to 3Sum to 2Sum
from typing import List
class Solution:
def fourSum(self, nums: List[int], target: int) -> List[List[int]]:
nums.sort()
results = []
if len(nums)<4:
return results
if sum(nums[:4])> target:
return results
if sum(nums[-4:])< target:
return results
for i, num in enumerate(nums[:-3]):
current_result = self.three_sum(nums[i+1:], target-nums[i])
current_result = [xi + [num] for xi in current_result]
results += current_result
results = [tuple(x) for x in results]
results = list(set(results))
results = [list(xi) for xi in results]
return results
def three_sum(self, nums, target):
results = []
if sum(nums[:3])> target:
return results
if sum(nums[-3:])< target:
return results
for i, num in enumerate(nums[:-2]):
current_results = self.two_sum(nums[i+1:], target-nums[i])
current_results = [xi + [num] for xi in current_results]
results += current_results
return results
def two_sum(self, nums, target):
# assume nums is sorted
n = len(nums)
i = 0
j = n-1
current_sum = nums[i]+nums[j]
results = []
if sum(nums[:2]) > target:
return results
if sum(nums[-2:]) < target:
return results
while i<j:
current_sum = nums[i]+nums[j]
if current_sum==target:
results.append([nums[i], nums[j]])
i +=1
elif current_sum < target:
i += 1
else:
j -= 1
return results
if __name__ == '__main__':
nums = [1,0,-1,0,-2,2]
target = 0
s = Solution()
y = s.fourSum(nums=nums,target=target)
print(y)
This solution works by:
- 📊 Sorting the array first
- ✂️ Pruning impossible cases early (if smallest 4 sum > target or largest 4 sum < target)
- 🔁 Using recursion to break down the problem
- 🎯 Handling duplicates with set conversion
Solution 2: Optimizing Two Sum with Early Return 🏃♂️
In our second solution, we made a key optimization in the two_sum function. By adding an early return when we find a match, we can speed up the process significantly!
What Changed:
- ⚡ Added
j -= 1for faster traversal - 🎯 Early return on match
- 🔄 Maintained the same overall structure
def two_sum(self, nums, target):
# assume nums is sorted
n = len(nums)
i = 0
j = n-1
current_sum = nums[i]+nums[j]
results = []
if sum(nums[:2]) > target:
return results
if sum(nums[-2:]) < target:
return results
while i<j:
current_sum = nums[i]+nums[j]
if current_sum==target:
results.append([nums[i], nums[j]])
i +=1
j -=1 # Since we dont need to care the duplicatesd
elif current_sum < target:
i += 1
else:
j -= 1
return results
The results speak for themselves:
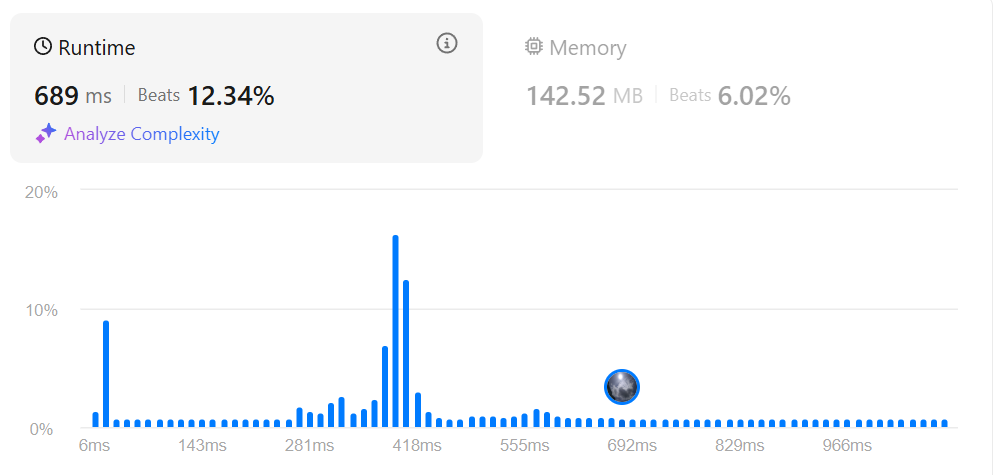
Solution 3: Smart Duplicate Handling 🧠
Our third solution introduces smart duplicate handling, which significantly improves performance by skipping redundant calculations.
Key Improvements:
- 🏃♂️ Skip duplicate values
- 🎯 More efficient pointer movement
- 💡 Smarter comparison logic
def two_sum(self, nums, target):
# assume nums is sorted
n = len(nums)
i = 0
j = n-1
results = []
if sum(nums[:2]) > target:
return results
if sum(nums[-2:]) < target:
return results
while i<j:
current_sum = nums[i]+nums[j]
if current_sum==target:
results.append([nums[i], nums[j]])
i +=1
while i < j and nums[i] == nums[i-1]:
i += 1
j -=1
while i<j and nums[j]==nums[j+1]:
j -= 1
elif current_sum < target:
i += 1
else:
j -= 1
Performance improvement shown here:
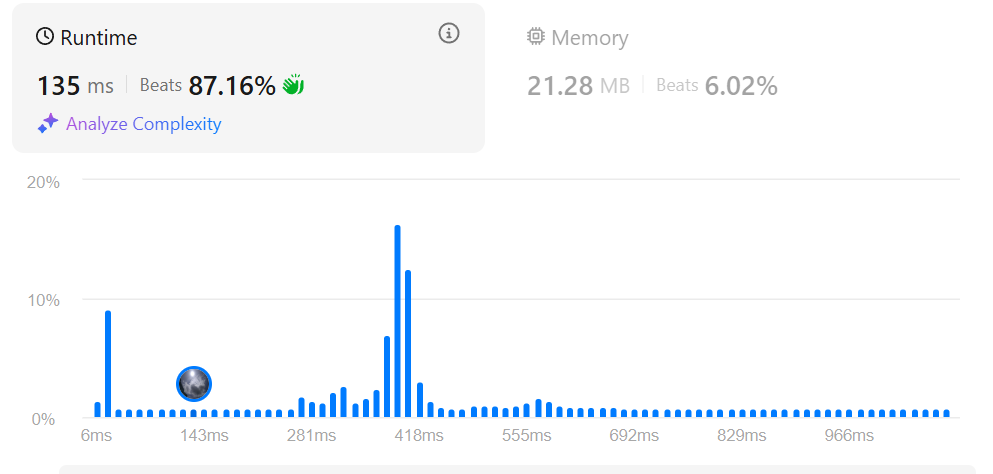
Solution 4: The Ultimate Optimization 🏆
Finally, we reached our most optimized solution using recursion with smart pruning and efficient duplicate handling.
Advanced Features:
- 🚀 Early termination conditions
- 🎯 Smart pointer management
- 🔄 Efficient recursive approach
- 🧮 Optimized memory usage
class Solution5:
def fourSum(self, nums, target):
def findNsum(l, r, target, N, result, results):
if r-l+1 < N or N < 2 or target < nums[l]*N or target > nums[r]*N: # early termination
return
if N == 2: # two pointers solve sorted 2-sum problem
results += [result+x for x in self.two_sum(l,r,nums, target)]
else: # recursively reduce N
for i in range(l, r+1):
if i == l or (i > l and nums[i-1] != nums[i]):
findNsum(i+1, r, target-nums[i], N-1, result+[nums[i]], results)
nums.sort()
results = []
findNsum(0, len(nums)-1, target, 4, [], results)
return results
def two_sum(self,l,r, nums, target):
results =[]
while l < r:
s = nums[l] + nums[r]
if s == target:
results.append([nums[l], nums[r]])
l += 1
while l < r and nums[l] == nums[l-1]:
l += 1
r -=1
while l<r and nums[r] ==nums[r+1]:
r -= 1
elif s < target:
l += 1
else:
r -= 1
return results
Final performance results:
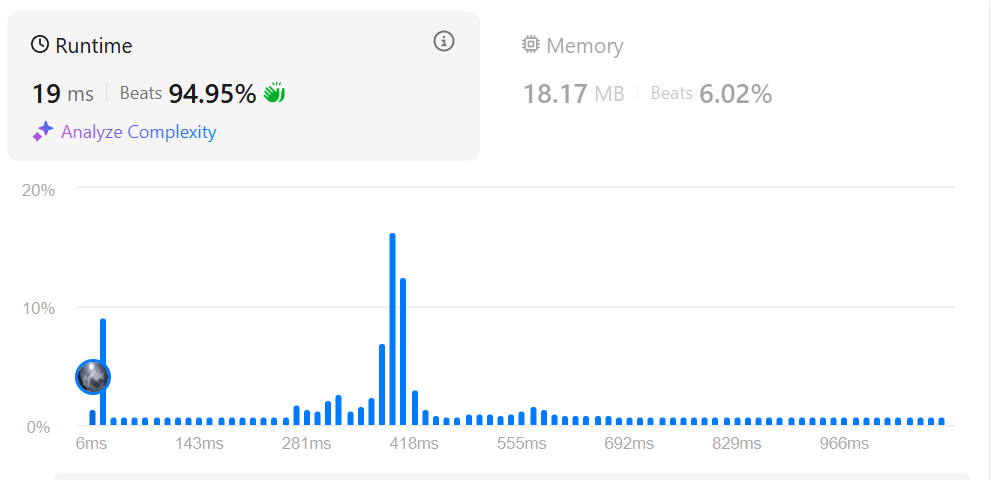
Time Complexity Analysis 📊
Let's break down the complexity of our solutions:
- Base Solution: O(n³) - Three nested loops with binary search
- Optimized Solution: Still O(n³) but with much better constant factors due to:
- Early pruning 🚫
- Duplicate skipping ⏭️
- Smart pointer management 👆
Key Takeaways 💡
- Early Pruning is crucial for performance
- Smart Duplicate Handling can significantly reduce unnecessary calculations
- Pointer Management is key in array problems
- Space-Time Tradeoffs are important considerations
Practice Tips 📝
- 🎯 Start with the basic solution and understand it thoroughly
- 🔄 Practice with different input sizes
- 🧪 Test edge cases carefully
- 📊 Compare performance with different approaches
Related Problems 🔗
Want to master array manipulation and sum problems? Here are some related LeetCode problems to practice:
Two Sum Family 👥
- Two Sum (Easy)
- The classic problem that started it all
- Find two numbers that add up to target
-
Great starting point for understanding the basics
-
Two Sum II - Input Array Is Sorted (Medium)
- Similar to Two Sum but with sorted input
- Uses two-pointer technique
- Good practice for optimizing with sorted arrays
Three Sum Family 👨👦👦
- 3Sum (Medium)
- Find triplets that sum to zero
- Natural progression from Two Sum
-
Introduces duplicate handling
-
3Sum Closest (Medium)
- Find triplet with sum closest to target
- Similar approach but different goal
- Good for understanding approximation problems
Four Sum and Beyond 👨👩👧👦
- 4Sum II (Medium)
- Four arrays instead of one
- Uses hash map approach
-
Different take on the 4Sum problem
-
K Sum (Hard)
- Generalized version for K numbers
- Tests understanding of recursive solutions
- Advanced problem combining multiple concepts
Similar Pattern Problems 🎯
- Combination Sum (Medium)
- Find combinations that sum to target
- Uses backtracking
-
Different approach to sum problems
-
Subarray Sum Equals K (Medium)
- Continuous subarray summing to target
- Uses prefix sum technique
- Different perspective on sum problems
Problem-Solving Tips for Sum Problems 💡
- Always consider sorting the array first if order doesn't matter
- Two-pointer technique is powerful for sorted arrays
- Hash maps can often optimize brute force solutions
- Watch out for duplicates and overflow cases
- Consider space-time tradeoffs in your solutions
Keep practicing these problems to build a strong foundation in array manipulation and algorithmic thinking! 💪